1. สัญลักษณ์ของเมทริกซ์
กลุ่มของจำนวนถูกเขียนเรียงเป็นแถว ๆ ละเท่า ๆ กัน จะถูกล้อมรอบด้วยวงเล็บใหญ่ [ ] หรือวงเล็บเล็ก ( ) เราเรียกสัญลักษณ์ดังกล่าวว่า เมริกซ์ เช่น
โดยทั่วไปเรานิยมเขียนเมทริกซ์ m × n
2. การเท่ากันของเมทริกซ์
เมทริกซ์ A และ B จะเท่ากันก็ต่อเมื่อ มีมิติเดียวกัน และสมาชิกที่อยู่ในตำแหน่งเดียวกันมีค่าเท่ากัน นั่นคือ
A = B ก็ต่อเมื่อ a11 = b11 , a12 = b12 เป็นต้น
ตัวอย่าง กำหนดให้
A = B ก็ต่อเมื่อ x= 1 และ y = 4 นั่นเอง
3. ทรานสโพสเมทริกซ์
At แทน ทรานสโพสเมทริกซ์ คือเมทริกซ์ที่เกิดจากการนำสมาชิกใน
เมทริกซ์A มาเปลี่ยนจากแถวเป็นหลักตามลำดับ
ถ้า A = [aij]mxn จะได้ At = [aji]nxm นั่นคือ การเปลี่ยนแถวเป็นหลักนั่นเอง
4. เมตริกซ์เอกลักษณ์
In แทนเมตริกซ์เอกลักษณ์มิติ n x n เช่น
I11 = 1 I12 = 0 I13 = 0
I21 = 0 I22 = 1 I23 = 0
I31 = 0 I32 = 0 I33 = 1
นั่นคือ เมื่อ Iij ; i = j จะมีค่าเป็น 1 และเมื่อ Iij ; i≠j จะมีค่าเป็น 0
5.
ถ้า A = [aij]mxn และ B = [bij]mxn
A+ B = [aij + bij ]mxn



จากตัวอย่างจะพบว่า

6. การคูณเมทริกซ์ด้วยสเกลาร์
สเกลาร์ คือ จำนวนจริง ให้ = c
cA = [caij]mxn
กำหนดเมทริกซ์
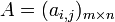 และจำนวน c เราสามารถนิยาม ผลคูณสเกลาร์ cA ว่าเป็นเมทริกซ์ขนาด
และจำนวน c เราสามารถนิยาม ผลคูณสเกลาร์ cA ว่าเป็นเมทริกซ์ขนาด  ที่คำนวณโดยการนำ c ไปคูณสมาชิกแต่ละตัวของ A กล่าวคือ หาก
ที่คำนวณโดยการนำ c ไปคูณสมาชิกแต่ละตัวของ A กล่าวคือ หาก 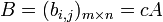 แล้ว bi,j = cai,j
แล้ว bi,j = cai,j ยกตัวอย่างเช่น
7. การคูณเมทริกซ์ด้วยเมทริกซ์
Amxp Bqxn = Cmxn
P ต้องเท่ากับ q จึงจะคูณได้
อธิบาย
ถ้า 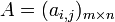 และ
และ 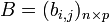 เป็นเมทริกซ์สองเมทริกซ์โดยที่จำนวนหลักของ A เท่ากับจำนวนแถวของ B แล้ว เราสามารถนิยาม ผลคูณ AB ว่าเป็นเมทริกซ์
เป็นเมทริกซ์สองเมทริกซ์โดยที่จำนวนหลักของ A เท่ากับจำนวนแถวของ B แล้ว เราสามารถนิยาม ผลคูณ AB ว่าเป็นเมทริกซ์ 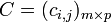 โดยที่
โดยที่ปฏิบัติการนี้อาจทำให้เข้าใจได้ง่ายขึ้นถ้ามองเมทริกซ์เป็นเวกเตอร์ของเวกเตอร์ โดยถ้าเราให้
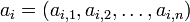 เป็นเวกเตอร์ที่มีสมาชิกเป็นสมาชิกในแถว i ของ A และให้
เป็นเวกเตอร์ที่มีสมาชิกเป็นสมาชิกในแถว i ของ A และให้ 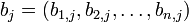 เป็นเวกเตอร์ที่มีสมาชิกเป็นสมาชิกในหลัก j ของ B แล้ว เราจะได้ว่า
เป็นเวกเตอร์ที่มีสมาชิกเป็นสมาชิกในหลัก j ของ B แล้ว เราจะได้ว่า  เมื่อ
เมื่อ 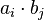 คือผลคูณจุดของ ai และ bj เช่น
คือผลคูณจุดของ ai และ bj เช่น- ให้
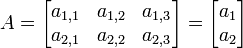 และ
และ 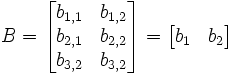
- แล้ว
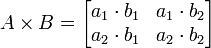
อ้างอิง
http://th.wikipedia.org/wiki
www.tutormaths.com/mathapa10.doc





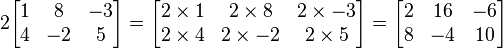
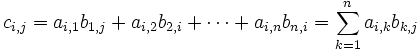



hi...
ตอบลบmy best friend...
you excellent
สุดยอดครับ
ตอบลบ